
To: MSI/NIS Science Team
From: Jeff Warren (warren@msss.com), Mike Malin (malin@msss.com)
Subject: Shot Noise Limiting Companding for MSI
Date: 8 February 1995
Introduction
Two 12-to-8-bit companding algorithms have been suggested for MSI: one
uses a simple linear mapping between 4095 and 255; the other attempts
to minimize the error introduced by the coarser bins when attempting
to reproduce the original 12-bit values from compressed data (i.e.,
minimizing the percentage difference between the original
12-bit input and a 12-bit value reconstructed from an 8-bit value).
One point that is overlooked in these algorithms is the impact of
nonlinear noise in the original 12 bit signal; that is, the photon
counting, statistical or "shot" noise. Since shot noise increases as
the square root of the signal, higher signal data have larger noise
levels (although they also have higher signal-to-noise ratios).
Linear, or lin-log companding, leads to an oversampling noisy data
while unnecessarily throwing away data that could otherwise be
resolved. This memorandum describes an algorithm for computing a
lookup table to optimally compand "noisy" 12 bit data to 8 bits while
introducing a minimal amount of quantization noise.
Noise Characteristics
For the purposes of this memo, a CCD will be considered a device for
counting electrons. A perfect device would be able to count the
electrons in the input signal and produce an exact replica as its
output. However, experiments that count items over an
interval of time (e.g., photons incident upon a CCD during a 100 ms
exposure) are subject to measurement fluctuations that result because
random samples of events distributed randomly in time contain numbers
of events that fluctuate from sample to sample. The likelihood of
observing any given number of counts is given by the Poisson
probability function, where the uncertainty is proportional to the
square root of the mean value.
In attempting to invert the observed count to infer the original
signal, the counting uncertainty introduces an uncertainty in the
reconstructed value. Table 1 shows an example of how uncertainty in
the counting statistics can affect the output signal. Note that in
Table 1 not only are the output values incorrect, they actually trend
in the direction opposite of the input signal. Since this attribute
of the data is independent of the efficiency of the device, it sets a
limit on the precision with which any measurement should be made. Any
additional precision is wasted, as one is then simply measuring
"noise."
Input Signal Max Counting error/Noise Example noise Output Signal
100 sqrt(100) = 10 +5 105
103 sqrt(103)=10.1489 -5 98
TABLE 1
Figure 1 shows in graphical form the "one-sigma" uncertainties
associated with a portion of a CCD's total range. Note the
significant overlap in the possible output values. The regions where
the uncertainty bars overlap represent output values that cannot be
mapped to distinguishable input values. In this example, an output
value of 100 has a finite probability of having been generated by an
original value as low as 91 and as high as 110. Even lower (and
higher) original values may also have been counted as 100, with lower
probability.

If two values in the output signal have uncertainty values that do not
overlap, the input signals that generated them are considered
discernible from one another, on the basis of statistical arguments
that values that differ by two-sigma are discriminable. Figure 1
illustrates this convention: consecutive or adjacent output signals
that vary from, for example, 90 to 115, are more likely to have been
caused by a real change in the input signal, while those that vary
from 92 to 108 are consistent with a constant input signal of 100 with
only a variation in the random noise. If one does not wish to retain
and quantify the high frequency variation in the output signal that
results from this statistical variation, the output signal can be
resampled to a coarser resolution which increases the probability that
transitions in the output signal represent real changes in the input
signal. Since this is a coarser sampling of the original output data,
a smaller number of bits can be used to represent this new output
signal.
Noise Limiting Quantization
A step function has been developed that resamples the original count
space into bins whose centers have a constant probability of being
discriminated from adjacent bins. Figure 2 shows graphically what the
resampling algorithm achieves. Stated explicitly, if the sqrt(N)
distribution about the input value represents a 1 sigma probability,
then this requantization ensures that the centers of adjacent bins
represent real changes in the input signal to a probability of 2
sigma.

The first bin is chosen such that its maximum value equals the "full
well" (the maximum possible number of counts) of the detector. For
the purposes of this discussion, it has been assumed that the
full-well count of the detector is equal to 500,000 electrons.
Other full-well values will give rise to different values for
resampling, as discussed at the end of this memo. For this example,
the center of the first bin (represented by No) is chosen
such that:
No + sqrt(No) = 500000
To solve this equation for No, a change of variables is
performed:
X = sqrt(No)
This yields the equation:
X^2 + X - 500000 = 0
This is simply a quadratic whose roots are given by:
X = { -1 +/- sqrt[1 + (4 * 500000)] } / 2
Having solved for X, No can now be computed as:
No = X^2 = 499293.393042
The next bin is then chosen such that its maximum value matches the
the minimum value of the first bin. The minimum value of the first
bin is given by:
k = No - sqrt(No) = 499293.393042 -
706.606958 = 498586.786084
The equation for the center of the next bin (represented by
N1) is then given by:
N1 + sqrt(N1) = k
This is the same equation used above to generate the first bin (when k
was equal to 500000). Thus, the center of each of bin can be computed
using the following equation:
X = { -1 +/- sqrt[1 + (4 * k)] } / 2
N = X^2
where k is initially 500000, and then subsequently set to X - sqrt(X)
for the next iteration.
Up to this point, this calculation has assumed that the CCD produces
counts at a resolution of 1 electron. Owing to limitations in
analog-to-digital conversion, the CCD's signal is actually quantized
into 4096 distinct levels. Assuming that the conversion from
electron counts to DN follows a linear relationship, and maps the
full-well value to the full 12 bit range, the actual signal
produced by the CCD is given by:
DN = N / S
DN = CCD output
N = original electron count
S = scaling constant = 4096 / 500000 = 122.0703
Values for N produced by the previous equations should be converted to
DN values using the equation above. As values for N become smaller,
multiple bin centers start mapping to the same value in DN space. At
this point, signal differences between the centers of DN values are
guaranteed to be discernible from one another and therefore no
quantization is necessary for smaller DN values.
Listing 1 shows the C code that implements the
algorithm just described. This program produces 677 bins in the
original 12 bit DN space that represent a noise limited approximation
to the original input signal. Table 2 shows the
results obtained by running this program.
At this point, the algorithm has requantized the dynamic range from
4096 levels (12 bits) to 677 levels (10 bits), preserving within the
data the ability to discriminate any two values with a confidence of
greater than 2-sigma.
Additional Quantization To 8 Bit Space
Owing to the nature of the MSI, the desired companding algorithm is
one that reduces the original 12 bits down to 8 bits using a single
lookup table. This can be achieved by sampling the 677 levels
previously determined at 256 regular intervals. Listing 2 shows the C code that implements this
sampling. In implementation, the order of the original 677 entry
table is reversed so that the first entry corresponds to the lowest
signal and the last entry corresponds to the highest signal. The
table is then divided into 256 bins using linear interpolation between
values in the original table to compute the values for the sampled
points. The reconstructed DN value for the center of each bin is
computed from the average of the bin's extents. Table 3 lists the output produced by this algorithm.
Columns 1 and 4 of this table can be used as the lookup table to
expand the data from 8 bits back to 12 bits. This table is easily
inverted to obtain the lookup table for converting from 12 bits to 8
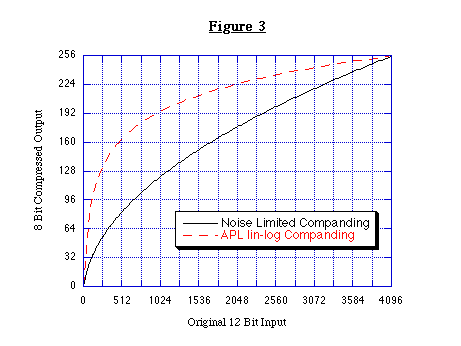
bits. Figure 3 shows the behavior of this companding algorithm as a
plot of the 8 bit values against the 12 bit values. For comparison,
the lin-log companding table proposed by APL is also shown.
Implementation Issues
It has been assumed that MSI is a fixed gain camera, that is,
that it converts the electron count to DN space by dividing by a
constant (full-well value / 4096 DN). Increases in exposure
time result in more electrons accumulating on the detector prior to it
being read out, but the size of the 4096 bins is a constant, and such
exposure variations only change which part of this linear space is
being used. Following the division, the DN values are forced to lie
in the range of 0 to 4095. This means that 0 electrons maps to
exactly 0 DN and the full-well value maps to exactly 4096 DN, which is
then clipped to 4095. If the scale factor for converting from
electron count to DN space is different from the one assumed
throughout this memo (i.e., if it isn't 500,000 electrons), then it
should be a simple matter to change the scale factor given in Listing 1. If the analog to digital conversion is
nonlinear, then the scaling equation in Listing
1 will need to reflect this more complicated function. In either
case, these changes should only affect the values in columns 3, 4 and
5 of table 2. After making these changes, the
quantization to 8 bit space should be performed the same way as
described to produce new values for Table 3.




