NEAR MSI Smear Correction Algorithm

Contents

Introduction

 The CCD of the NEAR MSI operates as a frame transfer system. Half of the detector is shielded so that it is not photoactive. After the exposure time has expired for an image, the photoactive portion of the detector is shifted into the other half of the detector for readout. Unfortunately, during this shifting of the data across the detector, the pixels of the CCD are still photoactive. Thus, during the time that it takes to perform the shift, the source signal is influencing the observed signal on the detector. Since the orignal image from the exposure has been shifted, the additional influence of the scene appears as a ghosting smear in the direction opposite of the shift. Figure 1 shows an example of this smear on a short exposure pinhole image that was acquired during the full instrument calibration testing of the MSI. Note that the diagonal artifacts in this image are electronic noise in the test setup and not part of the readout smear.

Figure 1

Correction Algorithm

Pat Murphy at APL devised an algorithm which performs an iterative process to reconstruct the original unsmeared image from the smeared image read out from the detector. The following describes the basis for her algorithm.

First, consider how light intensities are measured on the detector. Assuming that a pixel has linear response with exposure time, the signal at a pixel is given by:

Observed signal = (light intensity * exposure time) * pixel gain

light intensity = electrons / second
exposure time = seconds
pixel gain = DN / electrons
Considering a hypothetical system which consists of three pixels, the accumulation of signal over an exposure time of T is illustrated by the following diagram:

S0 = (L0 * T) * G0
S1 = (L1 * T) * G1
S2 = (L2 * T) * G2
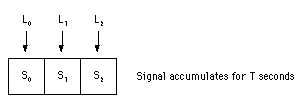
In a frame transfer system, half of the detector is physically masked off so that light cannot accumulate on the underlying pixels. This is necessary because the time that it takes to read values out of the detector can be quite long (~1 sec) relative to a short exposure time, however values can be shifted from one cell to another quite rapidly. Therefore, a frame transfer system shifts all the values from the photoactive cells of the detector to the masked cells very quickly, and then slowly reads the values out of the masked cells.

Figure 2 extends the three pixel system above to show how it would operate as a frame transfer device. This figure assumes that the original exposure time is T seconds and that the device can shift the pixels every dt seconds.

Figure 2

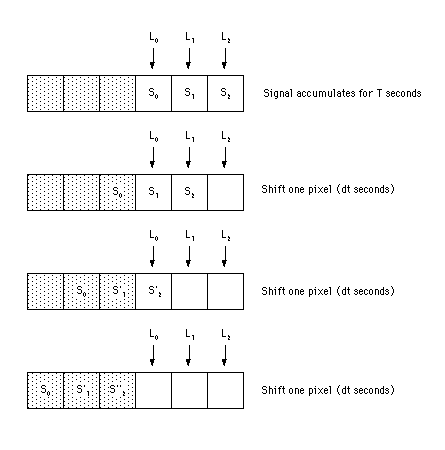
Once the values have been shifted into the masked cells, the process which reads the values out can be slow without concern of additional light accumulating on the cells. The main drawback of this approach is that during the shifting operation, additional signal is being added to each of the original values. Figure 2 shows that once the original values have reached the masked off area of the detector, the new values are given by:

S0' = S0
S1' = S1 + [(L0 * dt) * G0]
S2''= S2 + [(L1 * dt) * G1] + [(L0 * dt) * G0]

The additional signal that is added to each original value as it is shifted through the detector is what shows up as the smear in Figure 1. By rearranging the above equations it is possible to reconstruct the original values from the smeared output values, the exposure time, and the line transfer time: 


  S0 = [(L0 * T) * G0] = S0'

  S1 = [(L1 * T) * G1] = S1' - [(L0 * dt) * G0]
                       = S1' - [S0 * (dt / T)]

  S2 = [(L2 * T) * G2] = S2'' - [(L0 * dt) * G0] - [(L1 * dt) * G1]
                       = S2'' - [S0 * (dt / T)] - [S1 * (dt / T)]
                       = S2'' - [(dt / T) * (S0 + S1)]
These equations show that the general equation for reconstructing the original signal values is given by:
S(k) = smeared S(k) - (dt/T)*sum[S(0..k-1)]
Since it is assumed that S(0) is not smeared, then the smeared S(1) can be used to compute the unsmeared S(1) which in turn can be used to compute the unsmeared S(2), etc. In order to implement the algorithm for correcting MSI images, the line transfer time must be known and is given by:
number of active lines = 244
total time to transfer active lines = 0.9 msec
line transfer time = 0.9 msec / 244 lines = 0.0036885 msec/line
Using this line transfer time, the following algorithm performs the iterative process necessary to remove the smear from MSI images: 
	scale = (0.9 / 244) / exposure
	sum = 0
	for k = 1, nrow-1
		sum = sum + [scale*row(k-1)]
		row(k) = row(k) - sum
	endfor

Point Of Application

There was some discussion during the early stages of the MSI calibration effort as to when the smear correction step should be applied. Principally, should it be applied before or after the flat correction step? The original implementation had the smear correction performed after the flat correction.

From the equations shown above for S1' and S2'' it has been shown that the smeared signal values have the gains from multiple pixels convolved into them. Once the smear correction step has been applied, the resulting values only have the gain from the original pixel left in them. Therefore, smear correction must be applied prior to the flat correction step.

Example

The above algorithm was applied to the same image illustrated in Figure 1. The resultant smear corrected image is displayed in Figure 3. Note how efficient the algorithm was at removing the large smearing which was evident in the upper right pinhole image.

Figure 3

Availability

 Mark Robinson has trimmed down Pat's original IDL script for inclusion into the standard set of IDL scripts for processing NEAR images. Mark's IDL script is titled msi_smear.pro.